- 方法
- 有限差分时域法(FDTD)
FDTD 电磁模拟方法
随着问题规模的扩大,FDTD 方法具有出色的扩展性能。随着未知数数量的增加,FDTD 方法的效率很快就超过了其他方法。
手机型号由 Motorola Mobility, LLC/Lenovo 提供。
为什么使用 FDTD 仿真软件?
许多电磁模拟技术都是在频域中应用的,而 FDTD 则是在时域中求解麦克斯韦方程。这意味着电磁场值的计算是以离散的时间步骤进行的。时域方法的一个好处是,只需执行一次程序即可获得宽带输出;然而,使用 FDTD 方法的主要原因是,随着问题规模的扩大,该方法具有出色的扩展性能。随着未知数数量的增加,FDTD 方法的效率很快就超过了其他方法。FDTD 也被认为是对无线设备产生的生物效应进行电磁模拟的首选方法[1]。FDTD 方法已被证明是最有效的方法,可提供场穿透生物组织的精确结果。
简述 - FDTD 仿真基础知识
在 FDTD 方法中,空间和时间都被划分为离散的部分。空间被划分为箱形单元,与波长相比,箱形单元较小。如图 1 所示,电场位于盒的边缘,磁场位于盒的面上。这种场的方向被称为 Yee 单元 [2, 第 37 页],是 FDTD 的基础。时间被量化为一小步,每一步代表磁场从一个单元移动到下一个单元所需的时间。考虑到磁场与电场在空间上的偏移,磁场相对于时间的值也会发生偏移。电场和磁场的更新采用 "蛙跳式 "方案,即在每一步时间内首先计算电场,然后计算磁场。
当许多 FDTD 单元组合在一起形成一个三维体积时,就形成了一个 FDTD 网格或网格。每个 FDTD 单元都会与其相邻单元的边和面重叠,因此按照惯例,每个单元都会有三个电场,这些电场从与其相关的一个公共节点开始。FDTD 单元其他九条边上的电场属于其他相邻单元。如图 1 所示,每个单元还将有三个磁场,分别来自与电场共同节点相邻的单元面。
在网格中,可以通过改变给定位置的场计算公式来添加导体或电介质等材料。例如,在单元边缘添加完全导电的导线段时,由于完全导体的电场完全为零,因此计算电场的方程可以简单地设置为零。通过连接众多定义为完全导电材料的端对端单元边缘,就可以形成一条导线。引入其他材料或其他配置的处理方式与此类似,每种材料都可以根据材料的特性应用于电场或磁场。通过将许多单元边与材料相关联,可在 FDTD 网格内形成几何结构,如图 2 所示的介电球。图中每个小方框代表一个 FDTD 单元。
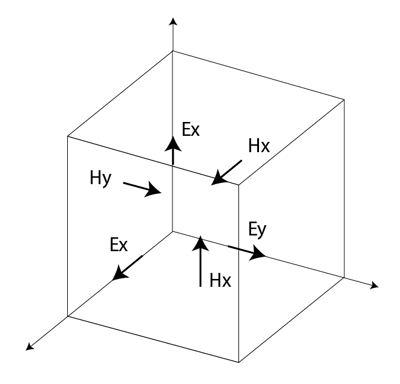
图 1:标有场成分的 Yee 小室

图 2:在传统 FDTD 网格中阶梯划分的介质球。各个单元边缘(电场位置)显示为重叠的网格线。
单元尺寸,即小盒子的尺寸,是任何 FDTD 仿真中最重要的约束条件,因为它不仅决定了时间步长,还决定了计算的频率上限。一般经验法则将最小分辨率以及频率上限设定为每波长 10 个单元。在实际应用中,单元尺寸往往小于此值,以便分辨待模拟结构的尺寸和特征,如基板厚度或导线长度。
激励可通过多种不同方式应用于 FDTD 仿真。一种方法是在一个或多个位置将采样波形应用于场更新方程,从而在离散位置模拟激励几何体。在时间的每一步,该时间段内的波形值都会添加到场值中。周围的场将根据每个单元的特性,在整个 FDTD 网格中适当传播引入的波形。计算必须持续进行,直到达到收敛状态。这通常意味着所有场值都已衰减到基本为零(从峰值至少下降 60 分贝),或已达到稳定状态。
细胞阶梯技术的进步
传统上,阶梯式 FDTD 单元在解决曲面或高变化场方面被认为是繁琐而低效的。FDTD 技术的进步使得保形网格和奇异性校正成为可能。
图 1 中的立方绮单元一般可以是矩形的。单元之间在 x、y 和 z 方向上的间距可以在整个问题空间内变化。这样就可以在强场区域(如高导电材料的小特征周围)放置更多的单元边缘。在一个单元内,FDTD 的标准更新方程可以通过多种方式进行细化,例如允许使用比单元尺寸更细的导线,或计算微带线等导体边缘的强场。另一种细化方法是允许物体的表面以相对于原理轴的任意角度与单元相交。这些 "共形 "单元可进一步细化,以考虑单元体积内物体表面的曲率。
图 3 显示了一部手机的几何形状。为了清晰起见,包括外壳在内的许多部件都被关闭,只显示天线附近的区域。图 4a 使用简单的矩形单元显示了手机 FDTD 网格的一小部分。图 4b 显示的是手机网格的同一部分,这次对包含物体表面部分的单元进行了保形处理。图 5 显示了保形网格表面的放大图。
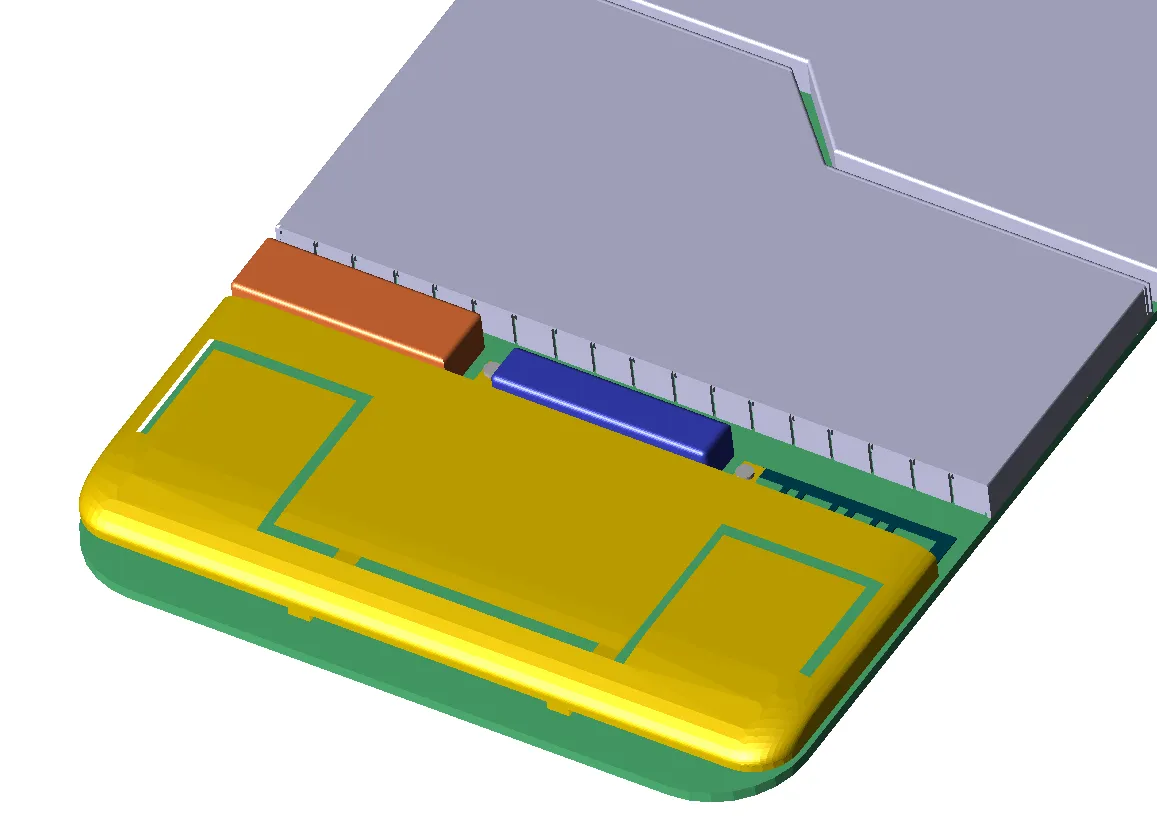
图 3:移动电话的天线部分。
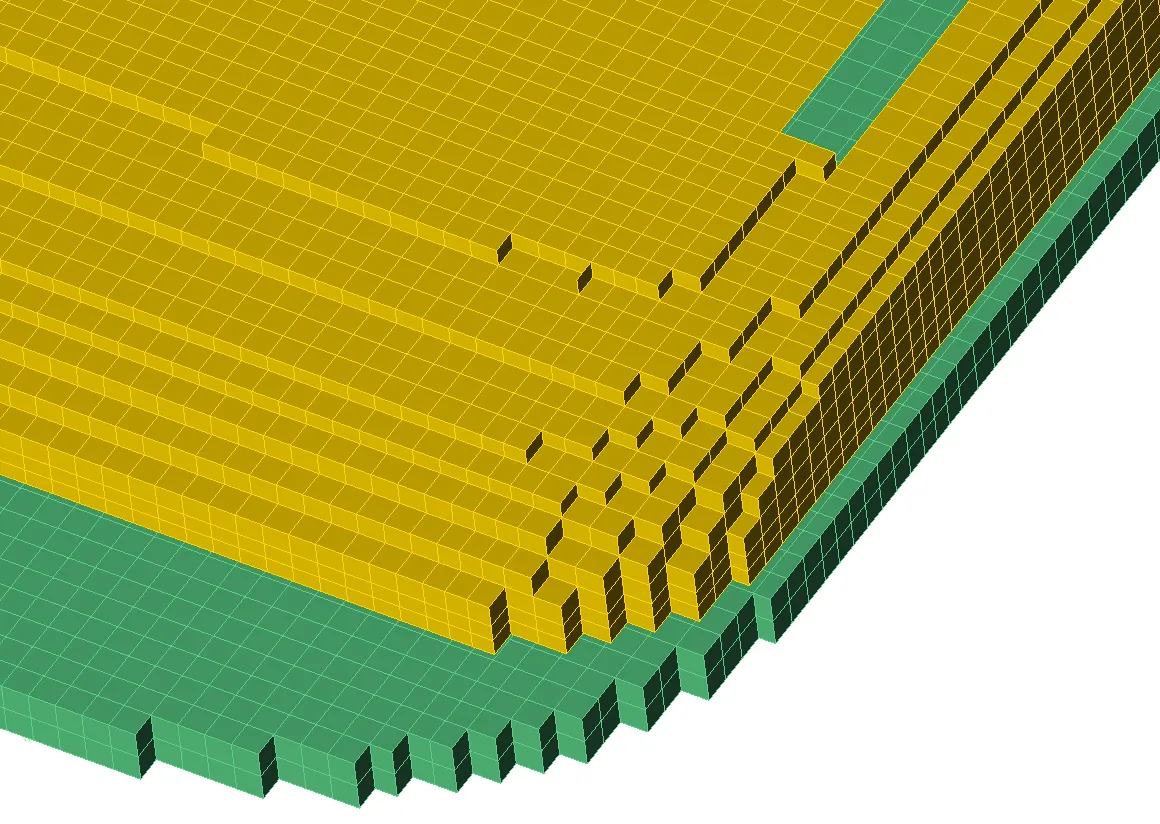
图 4a:使用简单矩形网格的天线角网格视图。

图 4b:采用共形网格的天线一角的网格视图。
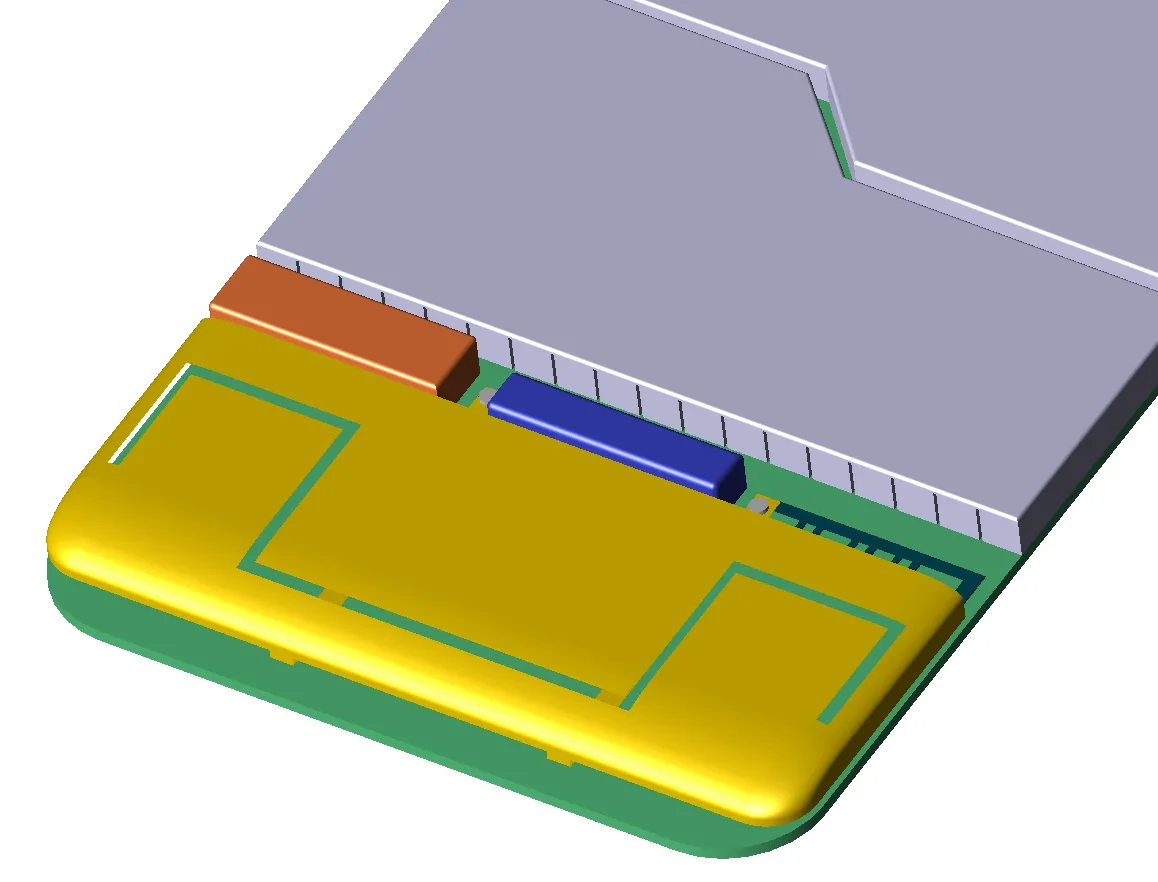
图 5:移动电话天线的共形网格。
材料
FDTD 模拟软件能够模拟各种电学和磁学材料。最基本的材料当然是自由空间。所有 FDTD 单元都被初始化为自由空间,除非添加其他材料来替代自由空间,否则所有单元边缘的场都将使用自由空间方程进行更新。
完全导电材料和磁性材料是通过将位于这些材料内的任何单元边缘的电场或磁场设为零来模拟的。由于这些材料的计算比较简单,因此在可行的情况下,最好使用完全导体而不是真实导体。铜等导体也可以在 FDTD 中进行模拟,但由于计算铜材料场的方程比完美导体的方程更复杂,因此计算时间会更长。当然,对于只有一小部分 FDTD 单元被定义为导体的情况,执行时间上的差异几乎不明显。
与频率无关的电介质和磁性材料是由其构成参数定义的,对于电性材料来说是相对介电率和电导率或损耗正切,对于磁性材料来说是相对磁导率和磁导率。在许多情况下,即使进行宽带计算,这些材料也是合适的,因为其参数在频率范围内变化不大。
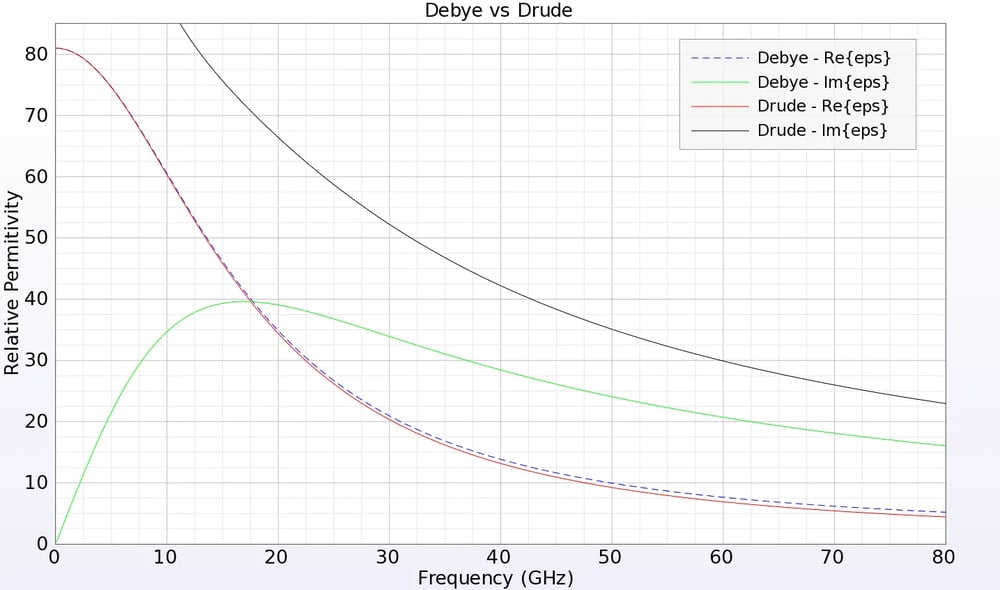
在某些情况下,与频率无关的材料并不合适,而应该用与频率相关的材料或色散材料来代替。频率相关材料的一些常见例子包括高含水量材料(如人体组织)、在光学频率下被激发的金属以及宽带电介质。XFdtd还具有模拟电性和磁性 Debye 和 Drude 材料(如等离子体、洛伦兹材料和各向异性磁性铁氧体)以及频率无关的各向异性介电材料的功能。这些材料的介电常数或磁导率在某些频率下可能为负,因此对宏观模拟超材料非常有效。FDTD 在模拟非线性材料方面也特别有效,XFdtd 中就包含了几种非线性材料。
近区与远区
对于任何给定的计算,被模拟结构的几何形状都是通过将特定位置的单元边缘设置为特定材料来定义的。整个 FDTD 几何空间(通常称为网格或网格)由这些单元的三维块组成。就数据存储而言,这个三维空间被视为 FDTD 中的近区区域。通过在 XFdtd 中保存一个 "近区 "点,可以观察到 FDTD 网格中任意边缘的场值与时间的函数关系。其他类型的数据,如稳态场幅、比吸收率、S 参数或阻抗等,也可针对网格内的适当点、面和体积进行存储。
可以制作足够大的 FDTD 网格,以便对几何体远场中的点进行采样。一般来说,这将耗费大量的计算机内存和计算时间,因为未知数(单元)的数量很可能很大。请注意,每个 FDTD 单元的最大尺寸为一个波长的十分之一,因此从结构上移动许多波长将需要大量单元。在大多数情况下,这并不是监测远场结果的合适方法。
将场值转换到远区以及计算辐射增益或雷达散射模式的一种更实用的方法是使用一种转换,将 FDTD 网格中的近区值转换为远离网格的某个位置的远场值。具体做法是将几何体围成一个方框,并将场存储在方框的外侧面上,以解决一般的远区问题。方框的面位于距离 FDTD 网格外边缘各五个 FDTD 单元的位置。要使变换有效,FDTD 几何体的所有部分都必须包含在方框内。
如图 6 所示,XFdtd 使用的极坐标系以 x 轴为方位角(phi),以 z 轴为仰角(theta)。该坐标系用于确定远区位置和入射平面波方向。
.webp?width=269&height=254&name=image-asset%20(4).webp)
图 6:远区和入射平面波方向所用的极坐标系。
宽带和稳态计算
一般情况下,FDTD 采用宽带计算,因为一次计算就能得出各种频率的结果,而不需要额外的计算机资源。当需要特定频率的数据时,可通过傅立叶变换从宽带计算中计算出稳态数据。
数据与频率对比的常见例子包括特定频率的天线模式、生物应用(如比吸收率 (SAR))、电场和磁场大小、磁通量大小、传导电流以及 "电路 "类型信息(如 S 参数、群延迟、阻抗、功率、效率等)。
在某些特殊情况下,例如避免在相关频率范围之外但靠近频率范围的强共振时,可能需要正弦激励。
外部辐射边界
三维单元网格构成了 FDTD 几何图形,每个单元位置的场更新都取决于相邻的场。然而,由于内存限制,网格必须在某一点结束,因此网格外缘的场无法正确更新。为了纠正这种情况,在 FDTD 网格的边缘应用了外辐射边界条件。
外辐射边界是一种吸收从 FDTD 网格向边界传播的场的方法。通过吸收这些场,网格似乎可以永远延伸。外部边界的性能是影响 FDTD 计算精度的重要因素,因此应注意正确使用外部边界。
在某些情况下,反射边界比吸收边界更可取。在 FDTD 计算中,可以使用完全导电的边界(电或磁)对场进行成像,以利用问题的对称性。周期性边界条件适用于模拟大型对称几何体的单个单元。
计算机资源
FDTD 是一种计算密集型方法,大多数合理的计算都需要一台快速计算机和至少几千兆字节的计算机内存。对于大多数应用而言,估算计算所需的计算机内存量相当简单。影响内存使用量和运行时间的最重要因素是用于表示被测结构的 FDTD 单元的数量。每个 FDTD 单元都有六个相关的场值:三个电场和三个磁场。此外,每个单元都有六个标志,分别表示六个场位置的材料类型。场值是实数,每个长度为 4 个字节,而标志每个长度为 1 个字节。这样,每个 FDTD 单元的内存使用量为:字段 24 字节,标志 6 字节,共计 30 字节。要估算以字节为单位的总内存需求,只需将 FDTD 单元数乘以每个单元 30 字节的数值即可。计算过程中会有一些开销,但一般都很小。一个明显的例外是宽带远区角,它为每个方向分配了六个一维实值数组。
估算 FDTD 计算的执行时间较为复杂,因为计算机处理器的性能各不相同。一种估算方法是计算需要执行的操作总数。在 FDTD 计算过程中,每个单元、每个时间步约有 80 次操作。根据单元数、时间步数和每个单元每个时间步 80 次运算系数的乘积,即可求出总运算次数。
如果知道处理器的浮点性能值,就可以计算出执行时间的值。不过,一般来说,更好的估算方法是确定一个简单问题在给定计算机上的执行时间,然后按所需计算与简单计算之间的运算次数比来计算时间。
有许多方法可以提高 FDTD 的计算速度,但其中一些方法需要大量的编程工作。其中最有效的方法是并行使用一台计算机的多个 CPU、并行使用多台计算机、优化缓存计算循环或利用 CPU 上的并行方法(如 SSE 和 AVX)。FDTD 软件尤其适合在 GPU 处理器上进行计算,因为许多单元并行执行数量相对较少的更新算法的概念与为更新视频显示而开发的方法非常契合。
参考资料
-
C95.3.2002, "Recommended Practice for Measurements and Computations with respect to Human Exposure to Radio Frequency Electromagnetic Fields, 100kHz to 300GHz," IEEE Standards and Coordinating Committee 28 on Non-Ionizing Radiation Hazards, April 2002.
-
K.K. S. Kunz 和 R. J. Luebbers,《电磁学的有限差分时域法》,佛罗里达州博卡拉顿:CRC Press,1993 年。

网络研讨会
模拟使用低地轨道卫星将 NB-IoT 覆盖范围扩展到农村地区
在本讲座中,Remcom 介绍了使用其 Wireless InSite® 射线跟踪仿真软件进行研究的结果,该软件可预测如何通过低地轨道卫星链路补充地面 5G 覆盖,以改善农村地区的 NB-IoT 覆盖。
探索 资源
出版物
XFdtd® 的新功能
XFdtd 7.11.1 版引入了多项增强功能,旨在提高仿真精度、扩展分析功能并简化工程工作流程。该版本反映了 Remcom 对解决天线设计、PCB 建模和相控阵系统开发中的高价值挑战的持续关注。
Explore Resource
网络研讨会
利用基于时间的移动性建立模型并模拟动态射频场景
敬请收看利用功能强大的无线预测和仿真平台 Wireless InSite 对动态射频环境建模的深入探讨。观众将了解如何在用户定义的场景中模拟收发器、天线和物体的移动,支持从地面通信系统到月球任务等各种应用。
探索 资源